二分查找

二分查找算法

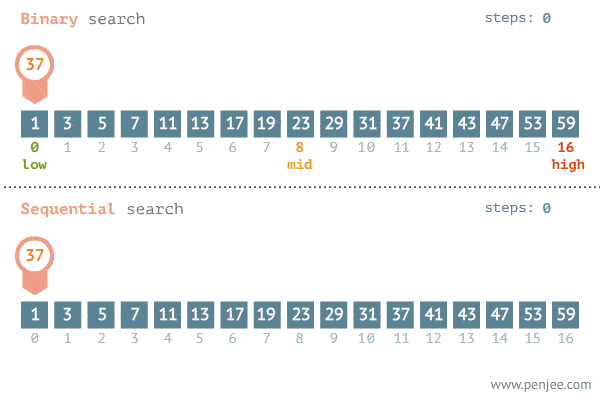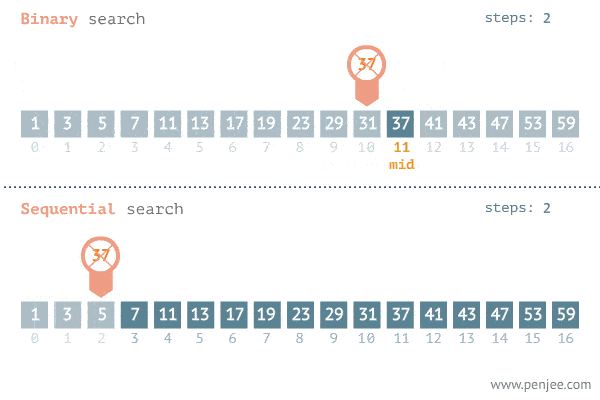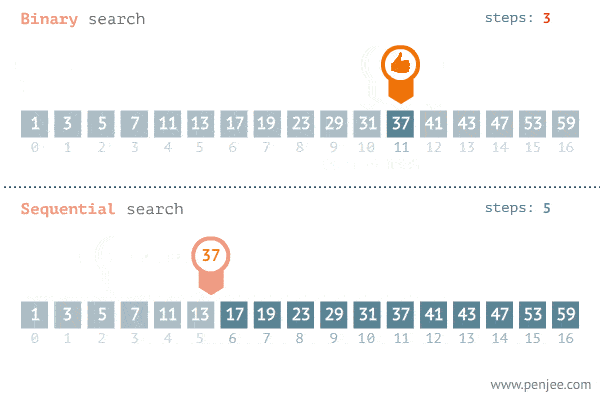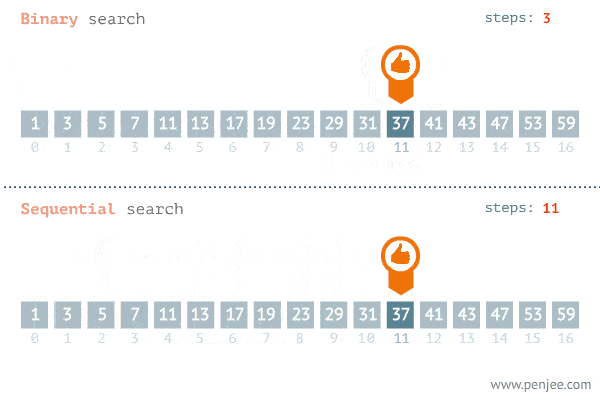
二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1

示例

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
1
2
3
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

解题

点击展开代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int search(int[] nums, int target) {
    int left = 0;
    // 定义target在左闭右闭的区间里，[left, right]
    int right = nums.length - 1;
    // 当left==right，区间[left, right]依然有效，所以用 <=
    while (left <= right) {
        // 防止溢出 等同于(left + right)/2
        int middle = left + ((right - left) / 2);
        if (nums[middle] > target) {
            // target 在左区间，所以[left, middle - 1]
            right = middle - 1;
        } else if (nums[middle] < target) {
            // target 在右区间，所以[middle + 1, right]
            left = middle + 1;
        } else {
            // nums[middle] == target
            // 数组中找到目标值，直接返回下标
            return middle;
        }
    }
    // 未找到目标值
    return -1;
}

第一个错误的版本

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例

1
2
3
4
5
6
7
输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false 
调用 isBadVersion(5) -> true 
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。
1
2
输入：n = 1, bad = 1
输出：1

提示

1
1 <= bad <= n <= 231 - 1

解题

点击展开代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int firstBadVersion(int n) {
    int left = 1, right = n;
    // 循环直至区间左右端点相同
    while (left < right) {
        // 防止计算时溢出
        int mid = left + (right - left) / 2;
        if (isBadVersion(mid)) {
            // 答案在区间 [left, mid] 中
            right = mid;
        } else {
            // 答案在区间 [mid+1, right] 中
            left = mid + 1;
        }
    }
    // 此时有 left == right，区间缩为一个点，即为答案
    return left;
}

搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例

1
2
3
4
5
6
7
8
输入: nums = [1,3,5,6], target = 5
输出: 2

输入: nums = [1,3,5,6], target = 2
输出: 1

输入: nums = [1,3,5,6], target = 7
输出: 4

提示

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 为 无重复元素 的 升序 排列数组
  • -104 <= target <= 104

解题

解法一

时间复杂度：O(n)
空间复杂度：O(1)

点击展开代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int searchInsertOne(int[] nums, int target) {
    for (int i = 0; i < nums.length; i++) {
        // 分别处理如下三种情况
        // 目标值在数组所有元素之前
        // 目标值等于数组中某一个元素
        // 目标值插入数组中的位置
        // 一旦发现大于或者等于target的num[i]，那么i就是我们要的结果
        if (nums[i] >= target) {
            return i;
        }
    }
    // 目标值在数组所有元素之后的情况
    // 如果target是最大的，或者 nums为空，则返回nums的长度
    return nums.length;
}

解法二

时间复杂度：O(logn)
时间复杂度：O(1)

点击展开代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static int searchInsertTwo(int[] nums, int target) {
    int left = 0;
    // 定义target在左闭右闭的区间里，[left, right]
    int right = nums.length - 1;
    // 当left==right，区间[left, right]依然有效，所以用 <=
    while (left <= right) {
        // 防止溢出 等同于(left + right)/2
        int middle = left + ((right - left) / 2);
        if (nums[middle] > target) {
            // target 在左区间，所以[left, middle - 1]
            right = middle - 1;
        } else if (nums[middle] < target) {
            // target 在右区间，所以[middle + 1, right]
            left = middle + 1;
        } else {
            // nums[middle] == target
            // 数组中找到目标值，直接返回下标
            return middle;
        }
    }
    // 分别处理如下四种情况
    // 目标值在数组所有元素之前  [0, -1]
    // 目标值等于数组中某一个元素  return middle;
    // 目标值插入数组中的位置 [left, right]，return  right + 1
    // 目标值在数组所有元素之后的情况 [left, right]，这是右闭区间，所以  return right + 1
    return right + 1;
}

相关文章

双指针